Planar Horseshoes (Dynamics Simulation)
ME 314 – Machine Dynamics
In the first quarter of my graduate program, I took a machine dynamics course, which focused on Lagrangian Mechanics, with all major coding assignments programmed in Python. This page highlights the final project completed at the end of the course.
Goals of the Project
For this project, the goal was to develop a planar simulation with:
- 2 to 5 degrees of freedom
- rotational inertia in the dynamics
- impacts of some sort
- external forcing of some sort
- an animation of the resulting simulation to show that it “works”
Proposal
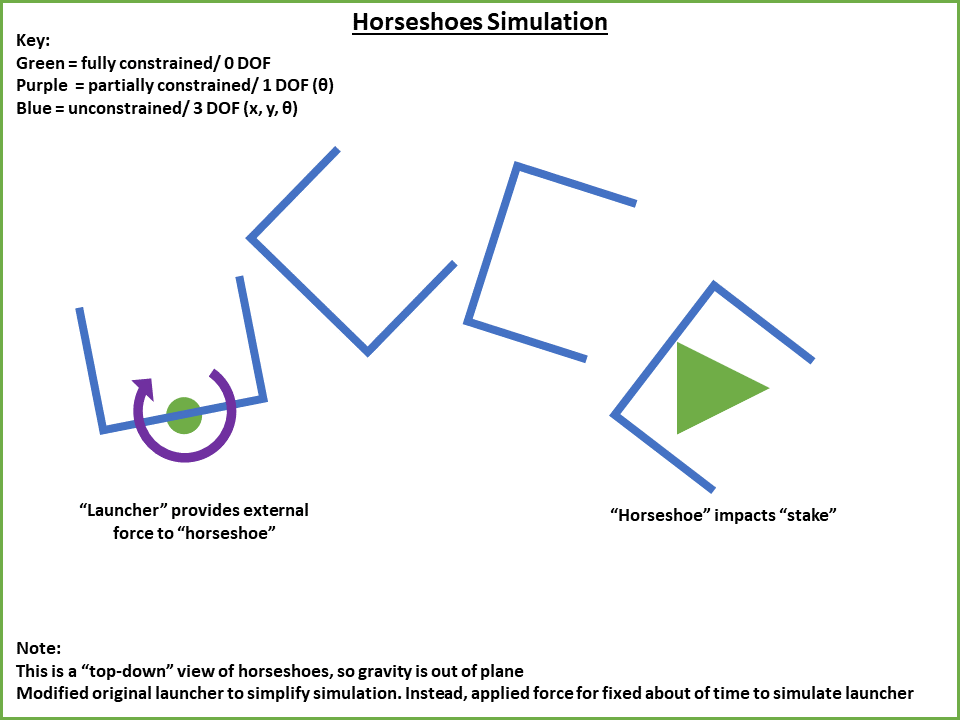
For my final project, I decided to simulate a planar version of horseshoes. To make the game planar, the horseshoe was thrown like a frisbee. This required a 1 DOF “launcher” to will release the horseshoe at a fixed condition. The “launcher” applied an angular acceleration to the horseshoe prior to release. After release, the horseshoe “flew freely” until it impacted the stake. The stake was be represented as a triangle.
Actual Simulation
To make the simulation work, I ended up simplifying the launcher to be an applied force to x and theta for a fixed duration (0.2s).
System Drawings
A sketch of the overall system is shown in the figure below:
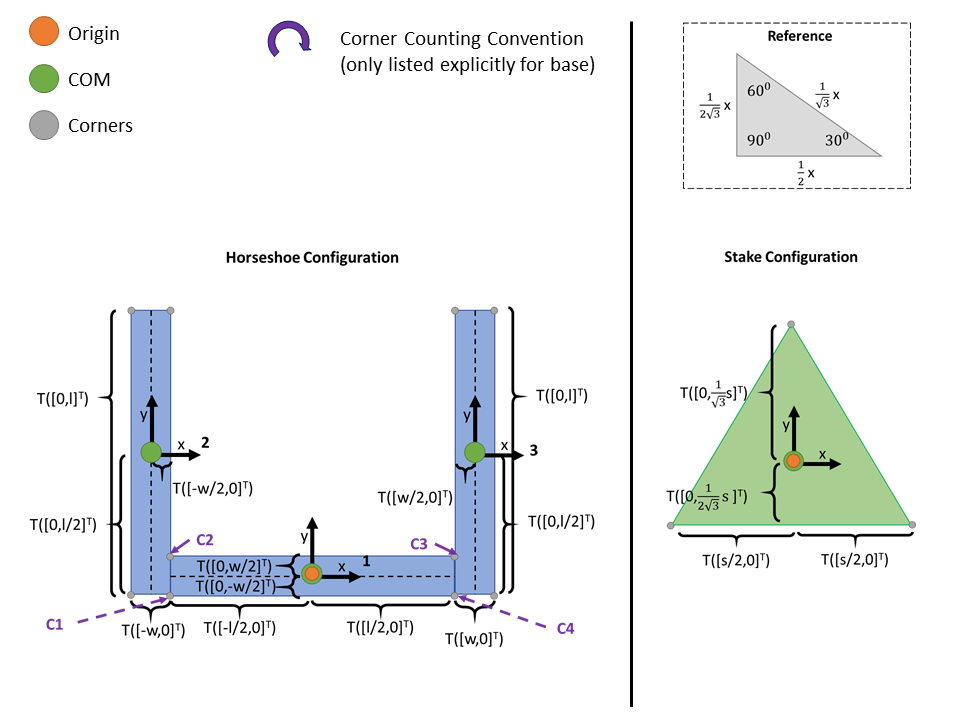
The rigid body transformations are shown in the figure below:
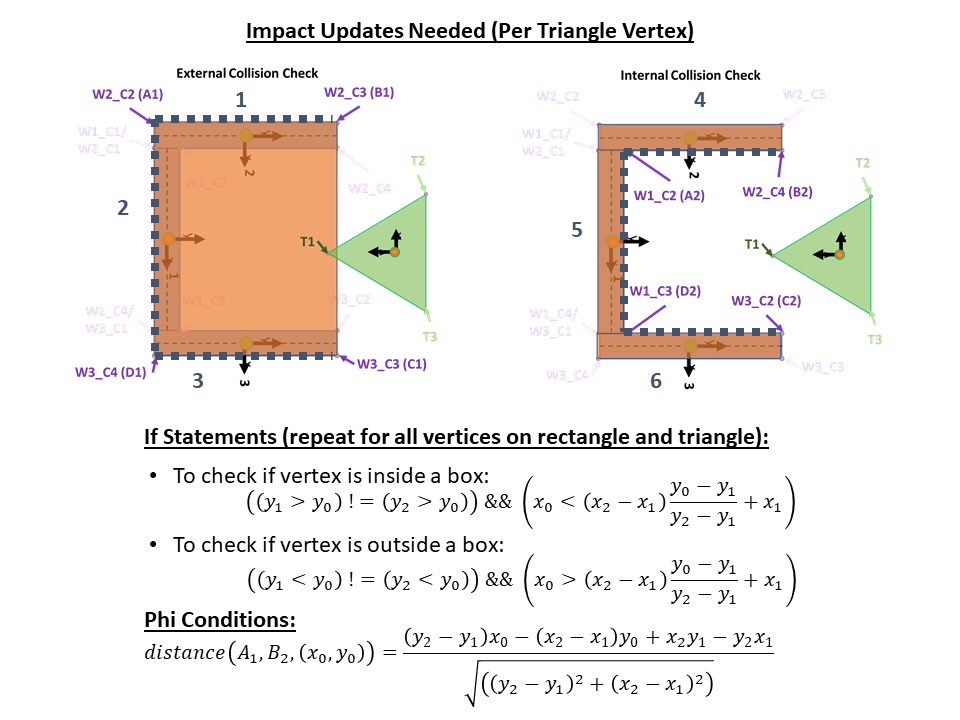
The impact updates are shown in the figure below:
Final Simulation
The Euler-Lagrange Equations are calculated for two different conditions:
- When the launcher is applying a force (Forced E-L Equations)
- After the horseshoe leaves the launcher
- The impact constraints and impact updates are described in the figure above. These are solved for numerically during the simulation
- The simulation also checks for impacts between vertices of the horseshoe and the sides of the stake (not explicitly listed in the figure above)
The animation plays back several different start angles for throwing horseshoes. The animation definitely appears to have the correct behavior for the outside of the horseshoe. I wasn’t able to fully debug the internal horseshoe collisions, but it appears to also be working properly by examining the animation.
The code and animation can be viewed on the following google colab document: https://colab.research.google.com/drive/15mrL_8np_BqLTyWcCcnX4Lx1PdBehYtS?usp=sharing